若手研究支援プログラム（J-PEAKS）

大規模な代数方程式系の計算、力学系の解析、コンピュータビジョン、耐量子暗号など幅広い応用で登場する。数値計算と異なり代数手法は厳密解を与えるため、システムの時間発展や応答特性、安定性などへの深い洞察を得られる。
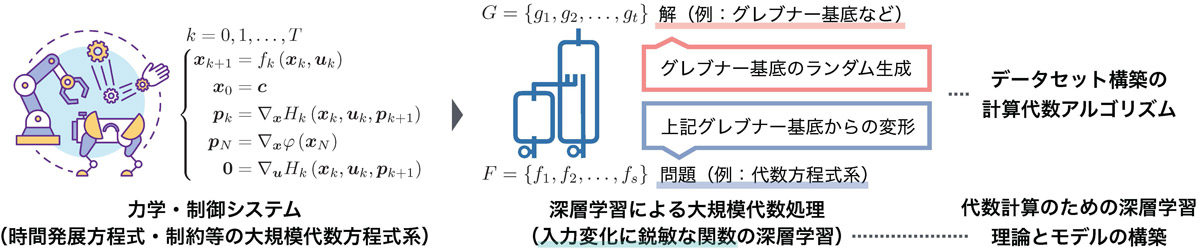
しかし多くの代数手法の基盤となるグレブナー基底の計算は、変数の数に対して指数的に計算量が増大する。本課題では、深層学習という新たな切り口でこの解決、特にその中心的役割を果たすグレブナー基底の計算の抜本的高速化を目指す。課題1では、データセット構築の代数。学習には例えば、代数方程式系とそのグレブナー基底の対(F,G)が必要である。
そのために、グレブナー基底Gを適当に得て、それを等価な適当な代数方程式系Fへと変形する。この従来と逆向きの問題は計算代数分野で未探索である。学習サンプルを効率的に生成可能な代数方程式系クラスの特定とその生成アルゴリズムを明らかにする。課題2では、入力鋭敏関数の学習。代数計算の学習には、入力される係数や演算記号一つの変化に対して鋭敏に関数の学習が求められる。

これに対応するため、入力鋭敏関数学習に向けた深層学習モデルの再設計とその理論的基盤の構築が行う。代数方程式系の計算が変数の数に対してスケールせず、現実規模のシステムへの適用が困難であることは長年の課題である。課題1, 2の解決はシステム制御分野のみならず、代数方程式系や微分方程式系の関わる広範な分野へ絶大な影響を与える。本研究構想は『学習』という新たな切り口から『学習のための計算代数』および『計算のための深層学習』という新領域を開拓する。

クリックで拡大表示

計良 宥志 助教の 記事 / ニュースリリース / インフォグラフィック